NeoFL-快速入门联邦学习

业务案例

​ 互联网企业A 为了提高用户对金融产品“小小贷”购买的转化率，想和金融企业B达成合作。互联网企业A有用户上网行为特征X1、X2、X3，金融企业B有用户的信用特征X4、X5和标签Y，这样就可以把两边的特征结合起来，并通过机器学习来提高“小小贷”购买的转化率。但是在合作的过程发现一个问题，那就是企业之间无法进行互通数据 ！！！

NeoFL概述

用户数据的隐私问题越来越受到重视，未来数据孤岛的问题也会越来越普遍，这对现有的传统机器学习的模式提出了挑战，因此一种全新的机器学习模式诞生了，那就是联邦学习。联邦学习源于2016年由谷歌正式提出的算法模型^[1]，在2017年^[2]首次定义了联邦学习。

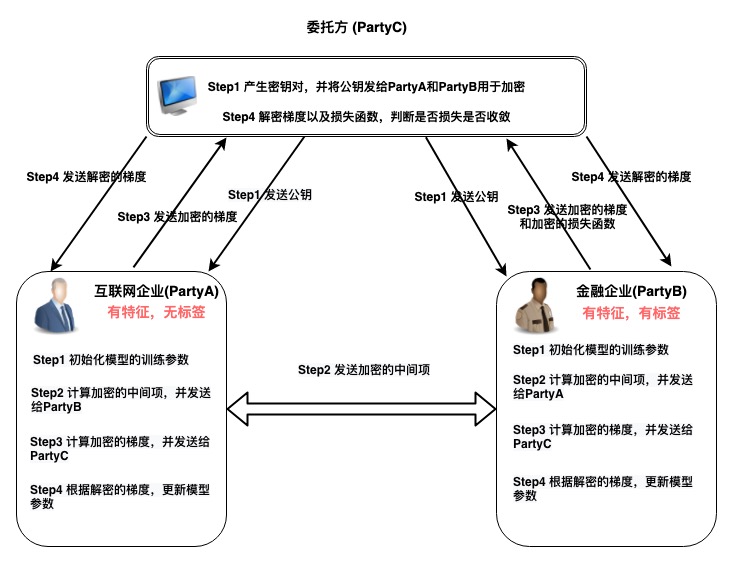
目前市面上存在一些开源的联邦学习框架，但每个框架都存在一定的问题，比如微众银行的FATE虽然称作是工业级的框架, 但配置多，操作起来特别复杂；百度提出的PaddleFL，存在初学者上手难，文档理解难的问题。因此本着取其精华弃其糟粕的想法，小编未依赖任何底层框架，从0到1手动实现了基于半同态加密的纵向联邦模式的逻辑回归算法框架 — NeoFL。我们通过NeoFL就可以解决最开始提出的企业之间无法进行互通数据的问题。NeoFL实现的大致流程如下图👇

算法介绍

符号说明

设有n个训练样本，Features和 Label分别表示成

$$X=\begin{bmatrix} x_{1}^T\\x_{2}^T\\\vdots\\x_{n}^T\\ \end{bmatrix} =\begin{bmatrix} x_{11} \cdots x_{1p}\\ \vdots \ddots \vdots\\ x_{n1} \cdots x_{np}\\ \end{bmatrix} =\begin{bmatrix} X_{A(n*k)} ｜ X_{B(n*(p-k))} \end{bmatrix}$$

和

$$y=\begin{bmatrix} y_{1}\\y_{2}\\\vdots\\y_{n}\\ \end{bmatrix}$$

其中$y=0$和$y=1$分别表示表示用户不购买和购买金融产品，$X$的每行代表每个用户的特征向量。

损失函数

逻辑回归模型的损失函数和梯度公式中包含指数运算，如果采用半**同态加密**算法，需要对原始的公式进行变换，使其变成只包含加法和数乘的形式，这里我们可以通过泰勒展开来对指数形式的表达式进行近似。

常用的逻辑回归损失函数为

$$\begin{aligned} l(\theta)&=\frac{1}{n}\sum_{i=1}^{n}(1+exp(-y_{i}x_{i}^{T}\theta))\\ \end{aligned}$$

根据$\begin{aligned} f(z)&=(1+exp(-z))\\ \end{aligned}$可以得到

$$\begin{cases} f(0)=log2\\ \\ f^{'}(0)=-\frac{1}{2}\\ \\ f^{''}(0)=\frac{1}{4}\\ \\ f^{'''}(0)=0 \end{cases}$$

那么$f(z)$在 $z=0$ 处的泰勒展开式可以写成

$$\begin{aligned} f(z)&=f(0)+ f^{'}(0)z+\frac{f^{''}(0)}{2}z^2+0+O(x^3)\\ &\approx log2-\frac{1}{2}z+\frac{1}{8}z^2 \end{aligned}$$

因此，将损失函数进行二阶泰勒展开

$$\begin{aligned} l(\theta)&=\frac{1}{n}\sum_{i=1}^{n}(1+exp(-y_{i}x_{i}^{T}\theta))\\ &\approx\frac{1}{n}\sum_{i=1}^{n}\{log2-\frac{1}{2}y_{i}x_{i}^{T}\theta+\frac{1}{8}y_{i}^2(x_{i}^{T}\theta)^2\}\\ &=\frac{1}{n}\sum_{i=1}^{n}[-\frac{1}{2}y_{i}(x_{iA}+x_{iB})^{T}\theta+\frac{1}{8}y_{i}^2\{(x_{iA}+x_{iB})^{T}\theta\}^2] + log2 \end{aligned}$$

那么损失函数的梯度表达式为

$$\begin{aligned} &\frac{dl(\theta)}{d\theta}=\frac{1}{n}\sum_{i=1}^{n}\{-\frac{1}{2}y_{i}x_{i}+\frac{1}{4}y_{i}^2(x_{i}^{T}\theta)x_{i}\}\\ \end{aligned}$$

根据PartyA和PartyB，将梯度分成上下两部分

$$\begin{aligned} \begin{bmatrix} \frac{dl(\theta)}{d\theta_A}\\ \\ \frac{dl(\theta)}{d\theta_B}\\ \end{bmatrix} &=\frac{1}{n}\sum_{i=1}^{n} \begin{bmatrix} -\frac{1}{2}y_{i}x_{iA}+\frac{1}{4}y_{i}^2\{(x_{iA}+x_{iB})^{T}\theta\}x_{iA}\\ \\-\frac{1}{2}y_{i}x_{iA}+\frac{1}{4}y_{i}^2\{(x_{iA}+x_{iB})^{T}\theta\}x_{iB}\\ \end{bmatrix} \\ &\\ &=\frac{1}{n} \begin{bmatrix}\frac{1}{4}\sum_{i=1}^{n} x_{iA}(x_{iA}^{T}\theta_A+x_{iB}^{T}\theta_B)-\frac{1}{2}\sum_{i=1}^{n}y_ix_{iA}\\ \\\frac{1}{4}\sum_{i=1}^{n} x_{iB}(x_{i}^{T}\theta_A+x_{iB}^{T}\theta_B)-\frac{1}{2}\sum_{i=1}^{n}y_ix_{iB}\\ \end{bmatrix} \\ &\\ &=\frac{1}{n} \begin{bmatrix}X_A^{T}(\frac{1}{4}X_A\theta_A+\frac{1}{4}X_B\theta_B)-\frac{1}{2}X_A^{T}y\\ \\ X_B^{T}(\frac{1}{4}X_A\theta_A+\frac{1}{4}X_B\theta_B)-\frac{1}{2}X_B^{T}y\\ \end{bmatrix} \\ & \\ &=\frac{1}{n} \begin{bmatrix}X_A^{T}(\frac{1}{4}X_A\theta_A+\frac{1}{4}X_B\theta_B-\frac{1}{2}y)\\ \\ X_B^{T}(\frac{1}{4}X_A\theta_A+\frac{1}{4}X_B\theta_B-\frac{1}{2}y)\\ \end{bmatrix} \\ \end{aligned}$$

这样就实现了分别在 PartyA 和 PartyB 计算梯度的目的。

流程

为了后续描述方便，我们将互联网企业A，金融企业B以及中间委托人C，分别命名为PartyA，PartyB以及PartyC

步骤	PartyA	PartyB	PartyC
Step1	初始化 PartyA模型的训练参数$\theta_A$	初始化 PartyB模型的训练参数$\theta_B$	生成秘钥对，并分发公钥🔑给
Step2	计算加密的中间项$[[\frac{1}{4}X_A\theta_A]]$，将其发送给PartyB	计算加密的中间项$[[\frac{1}{4}X_B\theta_B-\frac{y}{2}]]$，并将其发送给PartyA
Step3	计算加密的梯度$[[dA]] = [[X_A^T(\frac{1}{4}X_A\theta_A + \frac{1}{4}X_B\theta_B-\frac{1}{2}y ]]$，将带有随机项的加密梯度 $[[dA+RA]]$其发送给PartyC	计算加密的梯度$[[dB]] = [[X_B^T(\frac{1}{4}X_A\theta_A + \frac{1}{4}X_B\theta_B-\frac{1}{2}y]]$，将带有随机项的加密梯度 $[[dB+RB]]$其发送给PartyC	接收来自PartyA和PartyB的加密梯度项
Step4	根据解密的梯度获取$dA$，并更新 PartyA 的模型参数$\theta^{t+1} = \theta^{t} - \alpha*\frac{dA}{n}$	根据解密的梯度获取 $dB$，并更新 PartyB 的模型 $\theta^{t+1} = \theta^{t} - \alpha*\frac{dB}{n}$	将加密的梯度进行解密，并分别发送给PartyA和PartyB 计算解密后的loss，并判断loss是否收敛，若收敛增本轮迭代结束，否则重复Step2

实验

为了评估NeoFL中纵向联邦逻辑回归的效果，我们将未进行联邦学习的逻辑回归算法作为对照组，其中对照组中针对损失函数是否进行泰勒近似分成对照组1和对照组2。

本文是基于sklearn中的乳腺癌数据集生成的模拟数据来进行实验，通过使用相同的训练数据集进行模型训练，观察损失值的下降曲线以及在测试集上的模型效果。

损失变化

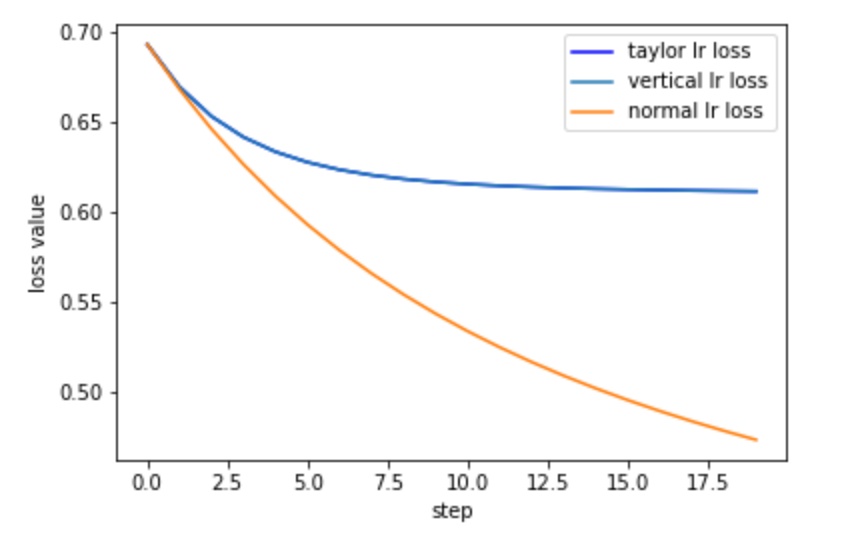
其中上述曲线中，横轴代表算法的迭代次数，纵轴表示每次迭代对应损失值，其中每条曲线的含义如下：

(1) vertical lr loss: 表示纵向联邦学习LR模型训练过程中的损失变化曲线；
(2) taylor lr loss: 表示标准的LR模型训练过程中的损失变化曲线，其中损失函数用泰勒展开来近似；
(3) normal lr loss: 表示标准的LR模型训练过程中的损失变化曲线。

模型效果

数据集	行数	特征数	纵向联邦LR的AUC	标准LR的AUC(泰勒近似)	标准LR的AUC
Breast Cancer	426	30	训练集：0.9921	训练集：0.9921	训练集：0.9895
Breast Cancer	123	30	测试集：0.9843	测试集：0.9816	测试集：0.9816

由上述的损失变化以及模型效果可以看到，与标准的逻辑回归相比，NeoFL的纵向逻辑回归算法在保证各方数据隐私性的同时，实现了模型效果没有损失的目的。

展望

针对目前的联邦学习框架，还有进一步的优化空间，比如：

1. 优化频繁通信带来的性能问题；
2. 优化模型训练时中间数据落盘的存储问题；
3. 增加惩罚项来缓解模型的过拟合，并解决增加惩罚项之后，损失会越来越大的问题。

参考文献

[1] H. Brendan M, Eider M. Federated Learning of Deep Networks using Model Averaging(2016). https://arxiv.org/pdf/1602.05629v1.pdf

[2] H. Brendan M, Eider M. Communication-Efficient Learning of Deep Networks from Decentralized Data(2017). https://arxiv.org/pdf/1602.05629.pdf

附录

在这一部分，小编向大家介绍下如何通过Python实现NeoFL中纵向联邦的逻辑回归算法🥳

参与方父类

我们首先需要创建各参与方的父类，主要用于保存模型的参数、中间的计算结果以及与其他参与方的连接状态

# 各参与方的父类
class Party:
    
    def __init__(self, config):
        
        # 模型参数
        self.config = config
        
        # 保存各参与方的基本信息
        self.data = {}
        
        # 保存与其他节点的连接状况
        self.other_party = {}
    
    # 与其他参与方建立连接
    def connect(self, client_name, target_client):
        self.other_party[client_name] = target_client
    
    # 向特定参与方发送数据
    def send_data(self, data, target_client):
        
        target_client.data.update(data)

参与方子类

参与方A：在训练过程中仅提供特征数据

# 参与方A: 在训练过程中，仅提供特征
class PartyA(Party):
    
    # 初始化，当需要继承父类构造函数中的内容，且子类需要在父类的基础上补充时，使用super().__init__()方法。
    def __init__(self, XA, config):
        super().__init__(config)
        self.X = XA
        self.theta = np.zeros(XA.shape[1]) # 将逻辑回归的训练参数theta初始化为1
        
        
    ## A: Step3部分，计算encrypt的中间项, 并发送给PartyB
    def send_encrypted_items(self, client_B_name):
        
        # 获取对应的密钥信息
        partyA_info = self.data 
        assert "public_key" in partyA_info.keys(), "Error: 在Step2中send_public_key部分, PartyA没有成功接收到ClientC的 'public_key'. "
        public_key = partyA_info['public_key']
        
        # 计算中间项 XA * thetaA 并进行加密
        za = np.dot(self.X, self.theta) # 得到n*1的向量
        ua = 0.25 * za
        za_square = za ** 2
        
        # 更新自己的加密信息
        encrypted_ua = np.asarray([public_key.encrypt(x) for x in ua])  # 针对向量中的每个元素进行加密
        partyA_info.update({"encrypted_ua": encrypted_ua})              # 将加密后的中间项1/4*XA * thetaA保存到partyA_info
        
        # 求平方后，将对应的dict发送给B，为啥需要za_square这个平方项目
        encrypted_za_square = np.asarray([public_key.encrypt(x) for x in za_square])
        data_to_B = {"encrypted_ua": encrypted_ua, "encrypted_za_square": encrypted_za_square}
        self.send_data(data_to_B, self.other_party[client_B_name])
        
    ## A: step4部分，计算加密的梯度，并发送给partyC 
    def send_encrypt_gradient(self, party_C_name):
        
        # 获取自身的基本信息：包括秘钥，加密的中间项
        dt = self.data
        assert "encrypted_ub" in dt.keys(), "Error: 在PartyB的Step3中 PartyA没有成功接收到PartyB发过来的'encrypted_ub'."
        
        encrypted_ub = dt['encrypted_ub']
        encrypted_u = dt['encrypted_ua'] + encrypted_ub
        
        # 加密后的损失函数梯度为, 数乘不会影响同态性，其中第二项是损失函数的惩罚项，用的self.theta是前一轮的参数, 后续可以删除self.config['lambda'] * self.theta 这一项
        # 这个惩罚项后续删除！！！+ self.config['lambda'] * self.theta 
        encrypted_dl_a = self.X.T.dot(encrypted_u)
        
        # 新增同维度随机项，并将其也用同样的方式进行加密
        mask = np.random.rand(len(encrypted_dl_a))
        public_key = dt['public_key'] # 走到这一步，一定能取到秘钥
        encrypted_mask = np.asarray([public_key.encrypt(x) for x in mask])  # 针对向量中的每个元素进行加密
        
        # 增加随机项后的梯度为
        encrypted_masked_dl_a = encrypted_dl_a + encrypted_mask
        
        # 将随机项保存，用于后续的解码
        dt.update({"mask": mask})
        data_to_C = {'encrypted_masked_dl_a': encrypted_masked_dl_a}
        
        # 将加密后的带有随机项的梯度发送给partyC
        self.send_data(data_to_C, self.other_party[party_C_name])
        
    ## partyA: 接收解密的梯度，更新参数，并开启下一轮迭代
    def update_model_theta(self):
        
        # 获取解密的梯度
        dt = self.data
        assert "decrypted_masked_dl_a" in dt.keys(), "在 partyC的step5中，PartyA没有成功接收到来自partyC的解密的梯度decrypted_masked_dl_a."
        decrypted_masked_dl_a = dt['decrypted_masked_dl_a']
        dl_a = decrypted_masked_dl_a - dt['mask']
        
        # 更新模型参数theta = self.theta - .config["eta"](学习率) / n * dl_a
        self.theta = self.theta - config["eta"] * dl_a / self.X.shape[0]
        return

参与方B：在训练过程中，提供特征和标签

# 参与方B: 在训练过程中，提供特征和标签
class PartyB(Party):
    
    def __init__(self, XB, y, config):
        super().__init__(config)
        self.X = XB
        self.y = y
        self.theta = np.zeros(XB.shape[1])# 将逻辑回归的训练参数theta初始化为1
        self.data = {}
        
    # Step3 接收PartyA中的加密项, 并将自己的加密项发送给A
    def send_encrypted_items(self, client_A_name):
        
        dt = self.data
        assert "public_key" in dt.keys(), "Error: 在Step2中send_public_key部分, PartyB没有成功接收到ClientC的 'public_key'."
        public_key = dt['public_key']

        zb = np.dot(self.X, self.theta)
        ub = 0.25*zb - 0.5 * self.y
        encrypted_ub = np.asarray([public_key.encrypt(x) for x in ub])

        # 更新自己的加密信息
        dt.update({"encrypted_ub": encrypted_ub})
        dt.update({"zb": zb}) # 用于后续计算加密的loss

        # 构造发送给A的数据
        data_to_A= {"encrypted_ub": encrypted_ub}
        self.send_data(data_to_A, self.other_party[client_A_name])
        
    # B: step4部分，计算加密的梯度，并发送给partyC 
    def send_encrypt_gradient(self,client_C_name):
        
        # 不考虑惩罚项+ self.config['lambda'] * self.theta
        dt = self.data
        assert "encrypted_ua" in dt.keys(), "Error: 在PartyA的Step3中 PartyB没有成功接收到PartyA发过来的'encrypted_ua'."
        encrypted_ua = dt['encrypted_ua']
        encrypted_u = encrypted_ua + dt['encrypted_ub']
        encrypted_dl_b = self.X.T.dot(encrypted_u) 
        
        # 新增同维度随机项(认为也是加密项)
        mask = np.random.rand(len(encrypted_dl_b))

        # 增加随机项后的梯度为
        public_key = dt['public_key'] # 走到这一步，一定能取到秘钥
        encrypted_mask = np.asarray([public_key.encrypt(x) for x in mask])  # 针对向量中的每个元素进行加密
        encrypted_masked_dl_b = encrypted_dl_b + encrypted_mask
        
        # 更新PartyB中的随机数
        dt.update({"mask": mask})
        
        assert "encrypted_za_square" in dt.keys(), "Error: 在PartyA的Step3中 PartyB没有成功接收到PartyA发过来的'encrypted_za_square'"
        encrypted_z = 4 * encrypted_ua + dt['zb'] # 这一项是4*0.25*XA*thetaA + XB*thetaB = XA*thetaA + XB*thetaB
        # 计算加密后的Loss
        encrypted_loss = np.sum( -0.5*self.y*encrypted_z + 0.125*dt["encrypted_za_square"] + 0.125*dt["zb"] * (8*encrypted_ua + dt["zb"]) )

        # 将加密后的B梯度以及加密后的loss保存成dict，并将其发送给clientC
        data_to_C = {"encrypted_masked_dl_b": encrypted_masked_dl_b, "encrypted_loss": encrypted_loss}
        self.send_data(data_to_C, self.other_party[client_C_name])
        
    ## partyB: 接收解密的梯度，更新参数，并开启下一轮迭代
    def update_model_theta(self):

        # 获取解密的梯度
        dt = self.data
        assert "decrypted_masked_dl_b" in dt.keys(), "在 partyC的step5中，PartyB没有成功接收到来自partyC的解密的梯度decrypted_masked_dl_b."
        decrypted_masked_dl_b = dt['decrypted_masked_dl_b']
        dl_b = decrypted_masked_dl_b - dt['mask']
        
        # 更新模型参数theta = self.theta - .config["eta"](学习率) / 
        self.theta = self.theta - self.config["eta"] * dl_b / self.X.shape[0]
        return

参与方C: 在训练过程中，提供秘钥对

class PartyC(Party):
    
    def __init__(self, XA_shape, XB_shape, config):
        super().__init__(config)
        self.A_data_shape, self.B_data_shape = XA_shape, XB_shape # 保存各参与方的数据维度
        self.public_key, self.private_key = None, None           # 保存公钥和私钥
        self.loss = []                                           # 保存训练中的损失值(用Taylor展开近似）
       
    # Step1 发送密钥对给partyA和partyB
    def send_public_key(self, party_A_name, party_B_name):
        
        try:
            public_key, private_key = paillier.generate_paillier_keypair()
            self.public_key = public_key
            self.private_key = private_key
            
        except Exception as e:
            print("PartyC 产生密钥对的过程失败, 详细失败原因: %s" % e)

        # 将公钥保存成字典的形式
        key_to_AB = {"public_key": public_key}
        
        # 将公钥分别发送给PartyA和PartyB, 更新相应对象的.data属性
        self.send_data(key_to_AB, self.other_party[party_A_name])
        self.send_data(key_to_AB, self.other_party[party_B_name])
        return 

    # Step5 将partyA和partyB发来的加密梯度进行解密, 并返回
    def send_decrypt_gradient(self, party_A_name, party_B_name):

        # 获取接收PartyA的加密梯度和PartyB的加密梯度
        dt = self.data
        assert "encrypted_masked_dl_a" in dt.keys() and "encrypted_masked_dl_b" in dt.keys(), "Error: 在 Step4 中 partyC 没有成功接收到来自 partyA 的'masked_dJ_a'或者来自 partyB 的'masked_dl_b'."
        
        encrypted_masked_dl_a = dt['encrypted_masked_dl_a']
        encrypted_masked_dl_b = dt['encrypted_masked_dl_b']
        
        decrypted_masked_dl_a = np.asarray([self.private_key.decrypt(x) for x in encrypted_masked_dl_a])
        decrypted_masked_dl_b = np.asarray([self.private_key.decrypt(x) for x in encrypted_masked_dl_b])

        # 将加密后的loss进行解密
        assert "encrypted_loss" in dt.keys(), "Error: 'encrypted_loss' 在Step4中 没有成功接收到来自 partyB 的'encrypted_loss'."
        encrypted_loss = dt['encrypted_loss']
        
        # 将加密后的loss进行解密
        # 计算解密后的loss，即除以n 再加上常数项log2
        # 不考虑惩罚项 #config['lambda']*(np.sum(decrypted_theta_a_square) + np.sum(decrypted_theta_b_square))/2*self.A_data_shape[0]
        loss = self.private_key.decrypt(encrypted_loss) / self.A_data_shape[0] + math.log(2) 
        print("******本轮迭代，计算的损失loss= ", loss, "******")
        self.loss.append(loss)
        
        # 针对至少迭代一次的loss开始进行判断，如果两次loss相减小于0.001，或者达到最大迭代次数max_iter，那么算法停止
        if len(self.loss) > 1 and (self.loss[-2] - self.loss[-1])<0.0001:
            return True


        data_to_A = {"decrypted_masked_dl_a": decrypted_masked_dl_a}
        data_to_B = {"decrypted_masked_dl_b": decrypted_masked_dl_b}
        
        # 将解密后的梯度发送给 partyA 和 partyB
        self.send_data(data_to_A, self.other_party[party_A_name])
        self.send_data(data_to_B, self.other_party[party_B_name])
        return

纵向联邦LR

训练基于半同态加密的纵向联邦逻辑回归模型

def vertical_logistic_regression(XA_train,XB_train,y_train,config):

    # Step1 将各参与方进行初始化
    party_A = PartyA(XA_train, config)
    print("参与方A 已成功初始化.")
    party_B = PartyB(XB_train, y_train, config)
    print("参与方B 已成功初始化.")
    party_C = PartyC(XA_train.shape, XB_train.shape, config)
    print("参与方C 已成功初始化.")


    # 将各个参与方进行连接, 本质上在每个客户端上, 将其他客户端的键值对{其他客户端别名: 其他客户端对象}保存到 other_party 这个属性中
    party_A.connect("neofl_B", party_B)
    party_A.connect("neofl_C", party_C)

    party_B.connect("neofl_A", party_A)
    party_B.connect("neofl_C", party_C)

    party_C.connect("neofl_A", party_A)
    party_C.connect("neofl_B", party_B)


    ## 开始训练, 根据配置的迭代次数
    for i in range(config['n_iter']):

        # Step2 生成秘钥并发送给客户端A和B,每次迭代都产生不同的秘钥
        party_C.send_public_key("neofl_A", "neofl_B")

        # Step3 互相传递加密部分
        party_A.send_encrypted_items("neofl_B")
        party_B.send_encrypted_items("neofl_A")

        # Step4 计算各自的梯度部分，并将其发送给partyC
        party_A.send_encrypt_gradient("neofl_C")
        party_B.send_encrypt_gradient("neofl_C")

        # Step5 接收A,B发来的加密梯度,并进行解密
        end = party_C.send_decrypt_gradient("neofl_A", "neofl_B")

        party_A.update_model_theta()
        party_B.update_model_theta()
        
        if end == True:
            print("提前终止迭代")
            break

        print(f"====== 第{i+1}轮迭代完成 =========== ")

    print("所有迭代全部完成 Success!!!")
    return party_C.loss, party_A.theta, party_B.theta

实验样例

# 加载数据并分成训练集和验证集
def load_data():
    
    # 加载数据
    breast = load_breast_cancer()
#     print("特征名称: ", breast.feature_names, len(breast.feature_names))
#     print("标签取值: ", breast.target_names, len(breast.target_names))

    # 数据拆分
    X_train, X_test, y_train, y_test = train_test_split(breast.data, breast.target, random_state=1)

    # 数据标准化
    std = StandardScaler()
    X_train = std.fit_transform(X_train)
    X_test = std.transform(X_test)
    return X_train, y_train, X_test, y_test


# 纵向分割数据, 将特征分配给A和B
def vertically_partition_data(X_train, X_test, A_idx, B_idx):
    """
    Vertically partition feature for party A and B
    :param X:      训练集特征数据
    :param X_test: 测试集特征数据
    :param A_idx: Party A 的特征索引
    :param B_idx: Party B 的特征索引
    :return: 分割后的训练特征数据XA_train, XB_train, 以及测试特征数据XA_test, XB_test
    """
    
    # 训练集分割，并在原始数组的起始部分，新增一列1
    XA_train = X_train[:, A_idx]  
    XB_train = X_train[:, B_idx]  
    
    
    # 测试集分割，并在原始数组的起始部分，新增一列1
    XA_test = X_test[:, A_idx]
    XB_test = X_test[:, B_idx]
    
    return XA_train, XB_train, XA_test, XB_test
    
    
# 导入数据，将数据分成训练和测试集，并标准化
X_train, y_train, X_test, y_test = load_data()
print("分割并标准化后的训练数据维度: {}行{}列".format(X_train.shape[0], X_train.shape[1]))

# 设置模型的配置参数
config = {
    'n_iter': 20,  # 迭代次数
    'eta': 0.05,  # 学习率
    'A_idx': [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29],  # PartyA 部分的特征索引
    'B_idx': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],                                                    # PartyB 部分的特征索引
} 

# 将数据集分成 PartyA 和 PartyB 部分
XA_train, XB_train, XA_test, XB_test = vertically_partition_data(X_train, X_test, config['A_idx'], config['B_idx'])
print('PartyA部分的数据规模:{}'.format(XA_train.shape))
print('PartyB部分的数据规模:{}'.format(XB_train.shape))

# 开始训练
fl_loss, fl_theta_a, fl_theta_b = vertical_logistic_regression(XA_train, XB_train, y_train, config)

为了与没有联邦学习的模型做对比，需要训练标准LR模型以及损失函数用泰勒展开近似的LR模型

# 标准逻辑回归
def normal_logistic_regression(X_train, y_train, X_test, y_test, config):
    
    # 参数初始化
    theta = np.zeros(X_train.shape[1])
    normal_loss_list = []
    
    ## 开始训练, 根据配置的迭代次数
    for i in range(config['n_iter']):

        # 计算梯度        
        dl=0
        for j in range(X_train.shape[0]):
            tmp = 1/(1+np.exp(y_train[j]*X_train[j,:].dot(theta)))
            dl += -tmp * y_train[j]*X_train[j,:]
        
        # 计算损失(去掉惩罚项)
        normal_loss = np.sum(np.log(1+np.exp(-y_train*X_train.dot(theta))))/X_train.shape[0]
        normal_loss_list.append(normal_loss)
    
        # 更新theta
        theta = theta - config['eta'] * dl / X_train.shape[0]
                      
    return normal_loss_list, theta
    
# 泰勒近似型逻辑回归
def taylor_logistic_regression(X_train, y_train, X_test, y_test, config):
    
    # 参数初始化
    theta = np.zeros(X_train.shape[1])# 将逻辑回归的训练参数theta初始化为1
    # 记录泰勒近似的损失函数
    taylor_loss_list = []
    
    ## 开始训练, 根据配置的迭代次数
    for i in range(config['n_iter']):

        # 计算梯度
        tmp = 0.25*X_train.dot(theta) - 0.5*y_train
        dl = X_train.T.dot(tmp)
        
        # 计算损失(去掉惩罚项)
        taylor_loss = np.sum(-0.5*y_train * X_train.dot(theta) + 0.125 * (X_train.dot(theta)*X_train.dot(theta)))/X_train.shape[0]  + math.log(2)
        taylor_loss_list.append(taylor_loss)
                      
        # 更新参数
        if len(taylor_loss_list)>1 and taylor_loss_list[-2]-taylor_loss_list[-1]<0.000001:
            print(f"前后两次迭代损失差为{taylor_loss_list[-2]-taylor_loss_list[-1]}, 提前终止迭代")
            break
    
        # 更新theta
        theta = theta - config['eta'] * dl / X_train.shape[0]
    
    # 获取最终的训练参数theta
    return taylor_loss_list, theta

最后，我们可以将联邦学习的LR，标准的LR以及带有泰勒近似的LR模型的预测结果进行比较

# 联邦学习LR训练
fl_loss, fl_theta_a, fl_theta_b = vertical_logistic_regression(XA_train, XB_train, y_train, config)

# 标准LR训练
norm_loss, normal_theta = normal_logistic_regression(X_train, y_train, X_test, y_test, config)

# 带有泰勒近似的LR训练
taylor_loss, taylor_theta = taylor_logistic_regression(X_train, y_train, X_test, y_test, config)


#模型效果评估
fl_y_prob = 1/(1 + np.exp(-XA_test.dot(fl_theta_a) - XB_test.dot(fl_theta_b)))
taylor_y_prob = 1/(1 + np.exp(-X_test.dot(taylor_theta)))
normal_y_prob = 1/(1 + np.exp(-X_test.dot(normal_theta)))

fl_y_train_prob = 1/(1 + np.exp(-XA_train.dot(fl_theta_a) - XB_train.dot(fl_theta_b)))
taylor_y_train_prob = 1/(1 + np.exp(-X_train.dot(taylor_theta)))
normal_y_train_prob = 1/(1 + np.exp(-X_train.dot(normal_theta)))

print("train fl lr auc", roc_auc_score(y_train, fl_y_train_prob))
print("train taylor lr auc", roc_auc_score(y_train, taylor_y_train_prob))
print("train normal lr auc", roc_auc_score(y_train, normal_y_train_prob))

print("test fl lr auc", roc_auc_score(y_test, fl_y_prob))
print("test taylor lr auc", roc_auc_score(y_test, taylor_y_prob))
print("test normal lr auc", roc_auc_score(y_test, normal_y_prob))

完整代码见👉：https://github.com/HuangNing616/neo_fl